Why Is Homomorphic Encryption Not Ready For Primetime?
By Priyadarshan Kolte | March 17, 2017
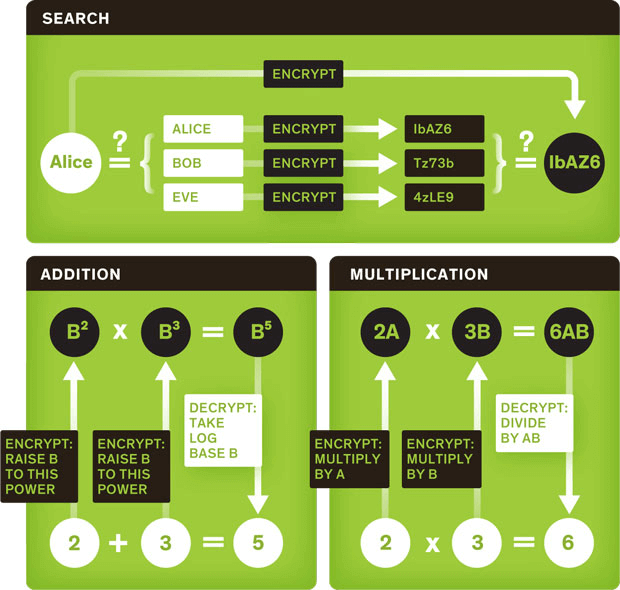
First a short lesson in history: In 1978, just a year after the RSA public-key scheme was developed, Rivest et al. published “On Data Banks and Privacy Homomorphisms” to explain how a small loan company (now known as a financial institution) could use a commercial time-sharing service (now known as a cloud provider) to store and compute on encrypted data. This influential paper led to the term Homomorphic Encryption (HE) for describing any encryption scheme where a particular operation on two ciphertext values gives an encrypted result that can be decrypted to get the result of some other operation on the plaintexts. Since the keys are needed only during initial encryption and final decryption, complete privacy of the inputs and outputs is maintained during the computation process. For example, if we use the Unpadded RSA encryption scheme to encrypt two plaintext values to get two ciphertext values, we see that that multiplying the two ciphertext values gives an encryption of the product of the two plaintext values. The El Gamal cryptosystem is similar to Unpadded RSA because multiplying two ciphertexts gives the encryption of the product of the plaintexts. As a different example, the Paillier encryption of two plaintexts gives two ciphertexts that can be multiplied to get an encryption of the sum of the two plaintexts. See figure to the right.
Since 1978, many encryption schemes have been discovered to have homomorphisms for various operations, but the question of whether any HE scheme performed both addition and multiplication operations on the plaintexts remained open for a long time. Such a scheme called Fully Homomorphic Encryption (FHE) would enable arbitrary computation on encrypted data through a sequence of additions and multiplications.
Download the Secure Data Sharing with SMPC White Paper
The existence of a FHE scheme was demonstrated in 2009 by Craig Gentry who constructed a scheme based on lattices. Gentry’s breakthrough was quickly followed by other researchers who published other FHE schemes. Although these FHE schemes allow arbitrary computation on encrypted data, the huge disadvantage is computation speed: the first FHE schemes were a trillion times slower than computation on unencrypted data. Speeding up FHE schemes is an active area of research with steady progress, and recent advances have brought the performance degradation to a factor of a million times slower. To sidestep the performance problems of FHE compared to HE, researchers Popa and Zeldovich who wanted to demonstrate practical performance in their CryptDB system resorted to using a suite of HE schemes consisting of Paillier and El Gamal encryption. The problem with using a suite of HE schemes where each HE scheme permits a specific operation is that each data has to be encrypted using the specific scheme that supports the specific operation on that data. This requires either the operations to be known in advance (at the time that the data is encrypted) or each data item has to be encrypted in multiple encryption schemes to permit multiple operations later. In any case, mixed operations (such as a sum of products) is not possible when using a suite of HE schemes instead of a single FHE scheme.
To summarize, the current homomorphic encryption schemes suffer from three limitations when it comes to impact to enterprise application to database workflows:
1. FHE schemes are extremely slow and require large memory compared to plaintext operations making them impractical for most database queries.
2. A suite of HE schemes requires prior knowledge of the type of queries to be performed so that the appropriate HE scheme can be selected to encrypt the raw data.
3. Unlike a single FHE scheme, a suite of HE schemes has restricted functionality, so some queries are not possible on encrypted data even if they are known in advance.
The promise of a practical homomorphic encryption scheme continues to entice cryptographers in academia, government and industry. The challenge issued by Rivest in 1978 has been conclusively answered in theory, and there is great progress since the first FHE scheme in 2009. However, in practice, the poor performance of full HE and the lack of support for all SQL operations in partial HE solutions makes it impractical to implement in enterprise environments any time soon.
Author bio:
Priyadarshan ‘PD’ Kolte is Co-Founder & CTO of Baffle, Inc., that provides encryption as a service for databases. He is a multi-core compiler expert with extensive experience in performance optimization and cryptography implementation techniques.